
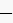

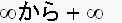 まで、周期的である事を、仮定している。(例2.も)
まで、周期的である事を、仮定している。(例2.も)前回は、周期的なディジタル信号から、周波数成分を求める公式を、使いました。
しかし、只、計算して、周期性を確認しただけです。内容は、よく解っていないです。
今回、
The Scientist and Engineer's Guide to Digital Signal Processing by Steven W. Smith, Ph.D.
と言う、書籍が、PDFで、公開されていたので、表題に揚げておきました。
(無償で、いい本が読める...うれしいです。 amazon.com でも、評価は5つ星ばっかりです。
この本は、加筆されて、
Digital Signal Processing: A Practical Guide for Engineers and Scientists]になっているそうです。 by amazom.com )
[私は、英語好きでも、なんでもありません。只、親切で、解りやすいから、読んでるだけです。ご了承下さいます様お願い申し上げます。]
この本の
Chapter 8 - The Discrete Fourier Transform
を、題材に、自分が何を計算していたのか? を、調べました。

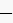

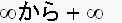 まで、周期的である事を、仮定している。(例2.も)
まで、周期的である事を、仮定している。(例2.も)
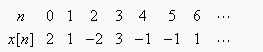 a
periodic signal
a
periodic signal
何故かと、言えば、
Stevenさんは、8章で(4/28ページ)
'What if you only have a finite number of samples stored in your
computer, say a signal formed from 1024 points. Isn't there a version of the
Fourier Transform that uses finite length signals? No, there isn't.'
'...As an alternative, the imagined samples can be a duplication of the actual 1024
points. In this case, the signal looks discrete and periodic, with a period of
1024 samples. This calls for the Discrete Fourier Transform to be used.'
知らんかった...無知でした...多謝多謝

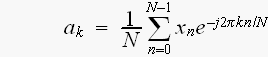
(from 'INTORODUCTORY DIGITAL SIGNAL PROCESSING by Paul/Wolfgang')
( ここから、Stevenさんの本からの引用)
'Periodic-Discrete
These are discrete signals that repeat themselves in a periodic fashion from
negative to positive infinity. This class of Fourier Transform is sometimes
called the Discrete Fourier Series, but is most often called the Discrete
Fourier Transform.'(この場合 the Discrete Fourier Seriesとも呼ばれるそうな...混乱してきた...)
ここで、basis functionsとは、(この章では、cosine と sine で、分けて考えています。)

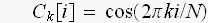

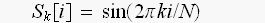 EQUATION
8-1
EQUATION
8-1
'Equations for the DFT basis functions. In these equations, 
![$C_{k}[]$](dsp10__7.gif) and
and 
![$S_{k}[]$](dsp10__8.gif) are the cosine and sine waves, each N points in length
are the cosine and sine waves, each N points in length
running from i=0 to N-1
The parameter, k, determines the frequency of the wave. In an N point DFT, k takes on values between 0 and . N/2.
...Since these sinusoids add to form the input signal, they must be the same length as
the input signal. In this case, each has 32 points running from 0 to 31.
The parameter, k, sets the frequency of each sinusoid .'
えーっと、複素数で考えたDFTの定義から、basis functions は

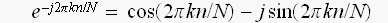 (Stevenさんの、iは、Lynnさんの言うところの、nに当たる)
(Stevenさんの、iは、Lynnさんの言うところの、nに当たる)
やから...
前節の例2.で、確かめてみましょう。

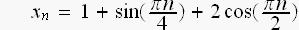

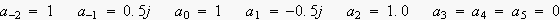
この場合 N=8 でした。
cosine は、周期が
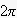 ですから、
ですから、
![$C_{k}[i]\quad $](dsp10__13.gif) の取り得る値は
の取り得る値は
i=0 から15まで代入して

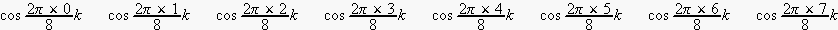

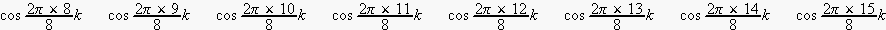


ですが、
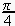 の整数倍の角度のcosineは、下記の5つの値しか、とらないから、上記は重複しています。
の整数倍の角度のcosineは、下記の5つの値しか、とらないから、上記は重複しています。

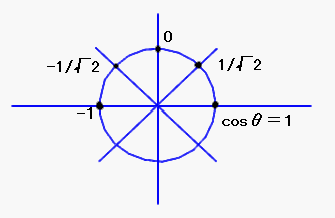
ですので、cosine のbasis functionsは5つでよい。
これを確かめるには、例えば

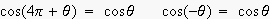 ですから,
ですから,

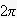 の整数倍kの2倍(
の整数倍kの2倍(
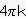 )を加えてもcosineの値は変わらないので、
)を加えてもcosineの値は変わらないので、
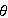 は符号を逆にして
は符号を逆にして

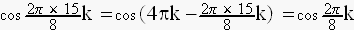
等々。
ですので、basis functionsは、今の場合

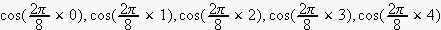
の、5つになると、思います。
sineも同様です。
結局、
N=8でサンルプリングされた、係数が実数の関数は
同数の、N=8
の要素を持つ(同じ数でサンプリングされた)、それぞれ、5つ(k=N/2+1)の
 の数列(cosine,sine)で、
の数列(cosine,sine)で、
表現できる事になります。
(これが、Lynn/Wolfgangさんの言っていた、ことやねんな...

 '
if x[n] is a real function of n, the values display a 'mirror-image' pattern
'
if x[n] is a real function of n, the values display a 'mirror-image' pattern

 real
parts of a
real
parts of a
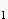 and a
and a
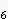 are equal,so are the those of \{a}
are equal,so are the those of \{a} 
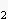 and a
and a
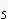 .
.

 The
imaginary parts shows a similar pattern,but with a change of sign.
The
imaginary parts shows a similar pattern,but with a change of sign.
This always happens when x[n] is a real function of n.')

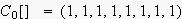

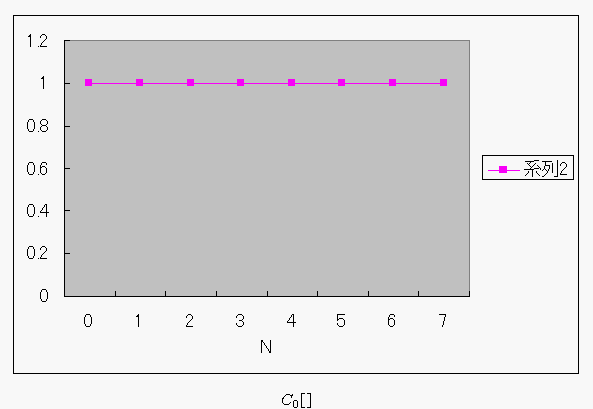

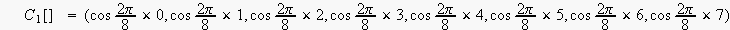

![]()

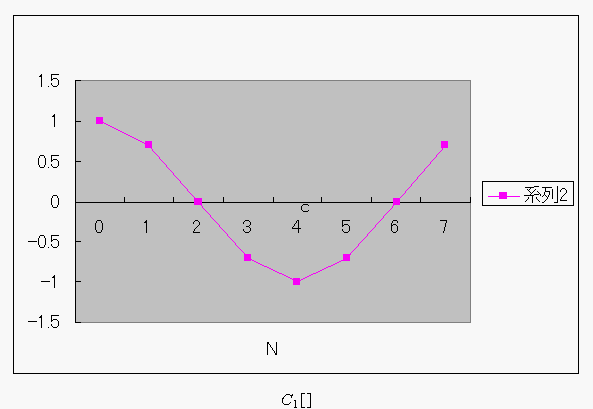

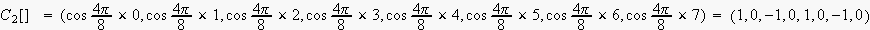

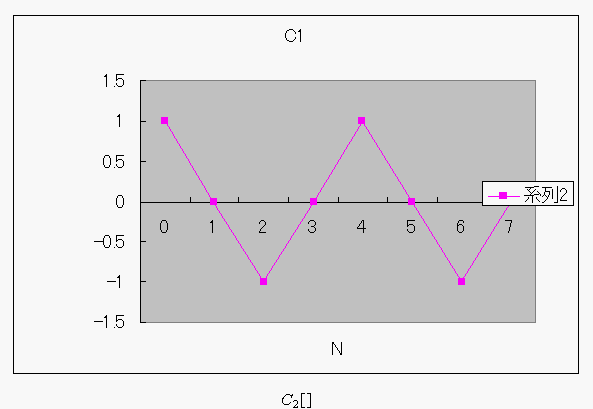



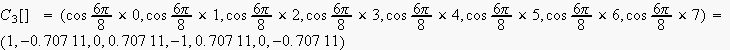

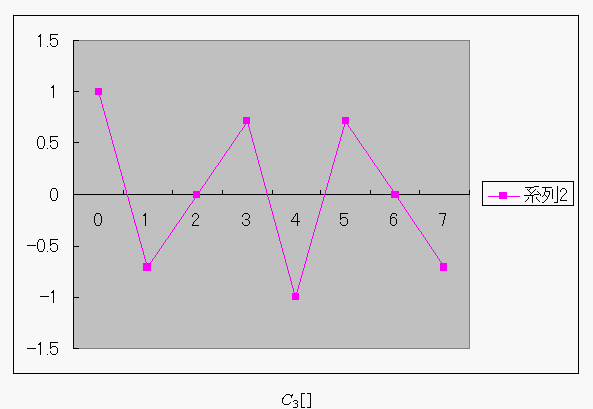
(点を結ぶだけでは、あかんみたい...)

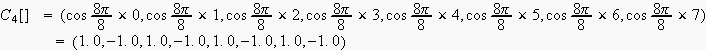

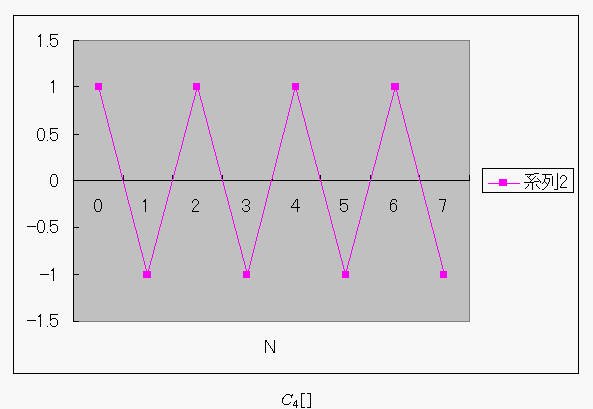
H.15.6.30
This document created by Scientific Notebook 4.1. この文書は次の製品で作成しました Scientific Notebook 4.1.