
![$\qquad x[n]=$](dsp3__1.png)

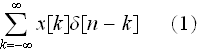
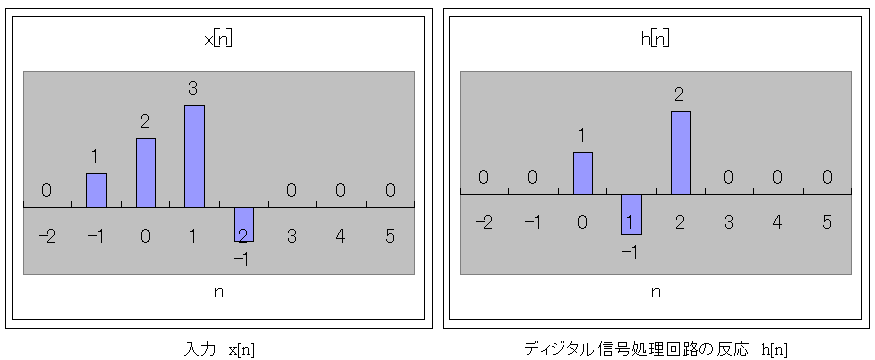
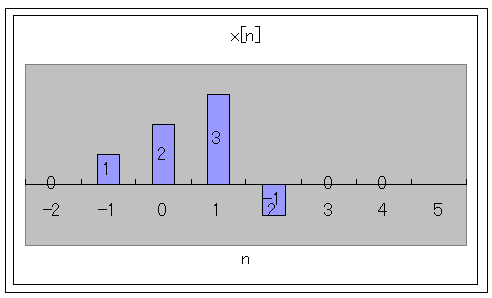
前回、ディジタル入力 x[n]、および、ディジタル信号処理h[n]を、インパルスで表現する事を、知りました。(時間軸に於いて)
そして、ディジタル入力x[n]の一般的な表現式は

![$\qquad x[n]=$](dsp3__1.png)

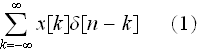
でした。
実は、これより、出力 y[n]は、すぐ出てきます。

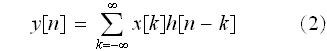
(1)式の
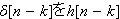 (離散的な信号処理の関数)に、置き換えるだけです。
(離散的な信号処理の関数)に、置き換えるだけです。
何故か?

前回、
例1では、我々は、次の出力を得ました。
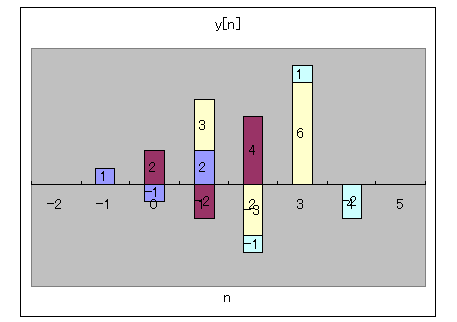
合計する前
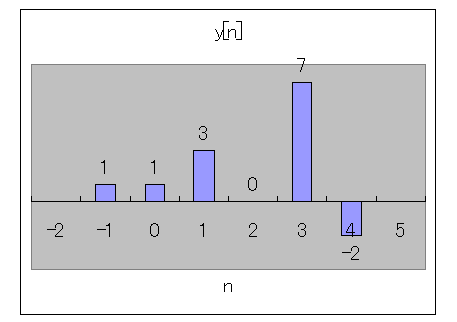
合計した出力
h[n]を
 で表現すると、
で表現すると、

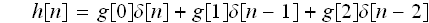
でした。
例1では

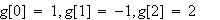 です。
です。
では、y[1」を求めてみましょう。
(2)式より

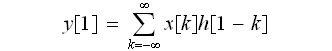
です。
合計する前の出力y[n]の図より、
n=1に関係する項は、k= -1,0、1の3つです。

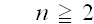 では、n=1の時に、影響を及ぼさないし、
では、n=1の時に、影響を及ぼさないし、
 信号処理のインパルスは、今の場合、3つだから、n
信号処理のインパルスは、今の場合、3つだから、n
 1で、x[n]は、3つ取ればよい
1で、x[n]は、3つ取ればよい

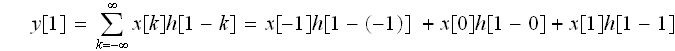

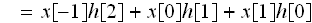
ここで、h[n]を
 で表現したものは
で表現したものは

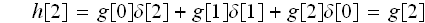

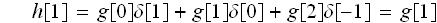

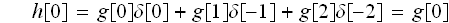
何故なら、

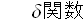 は
は
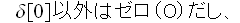

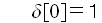
だから。
上式は

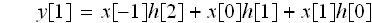

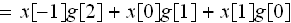

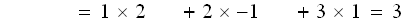
出ました!
同じようにして

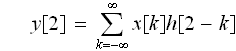

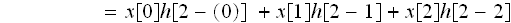

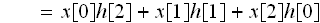

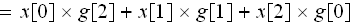

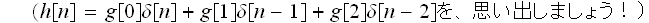



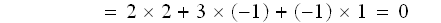
と、出ます。
以下、同じです。
上記の結果から

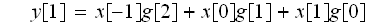

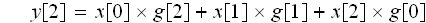
でした。
3つのx[n]を並べ、g[n]を逆に掛けていっています。
これを図から、理解して行きましょう。

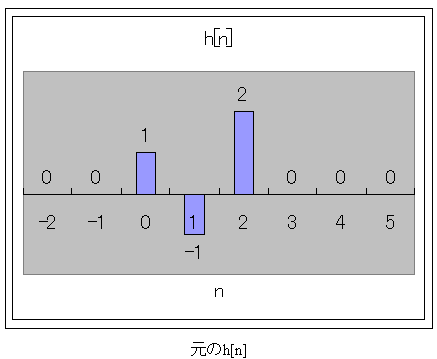
目盛りは、左から右に向かって、数字が増えて行ってます。
ですので、
目盛りを、逆に、右から見てやれば、よいのでは...
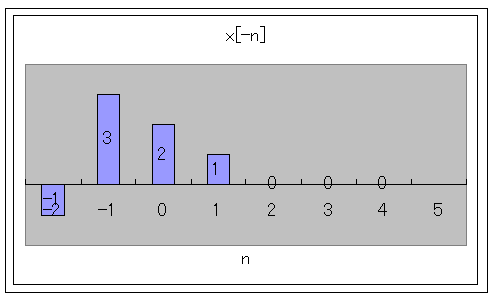
ですので、h[-n]を考えてみます。
元のh[n]は
h[0]=1、h[1]=-1、h[2]=2
ですので、この関係を壊さないようにして、h[-n]を考えます。
n=0の時 h[-0]=1
n=-1の時 h[-(-1)]=h[1]=-1
n=-2の時 h[-(-2)]=h[2]=2
ですから、図示すると

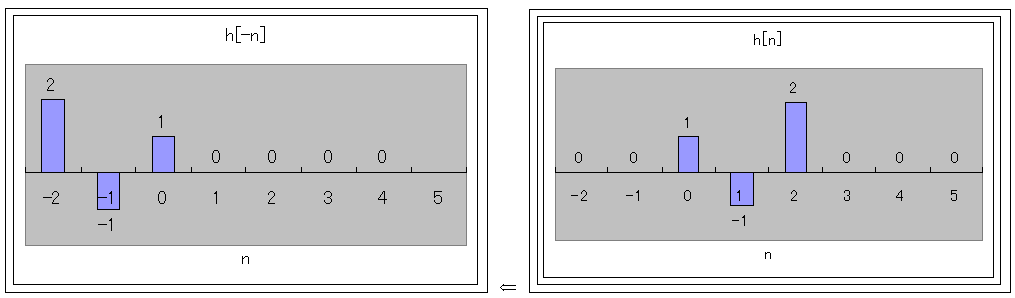
ですので、逆のインパルスはh[-n]になります。
このh[-n]を、更に1つずらします。
h[1-n]を求めるのです。
n=-1の時 h[1-(-1)]=h[2]=2
n=0の時 h[1-0]=-1
n=1の時 h[1-1)]=h[0]=1
これは、
h[-n]を1つだけ、右にずらす事になります。

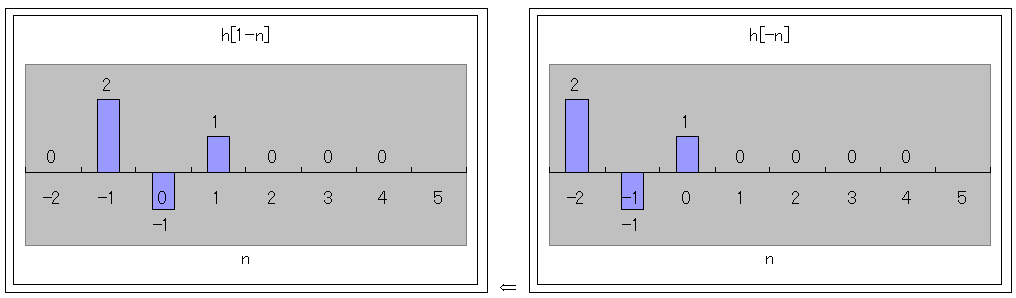
これで準備ができま縦した。
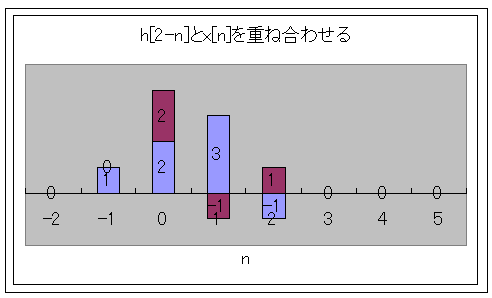
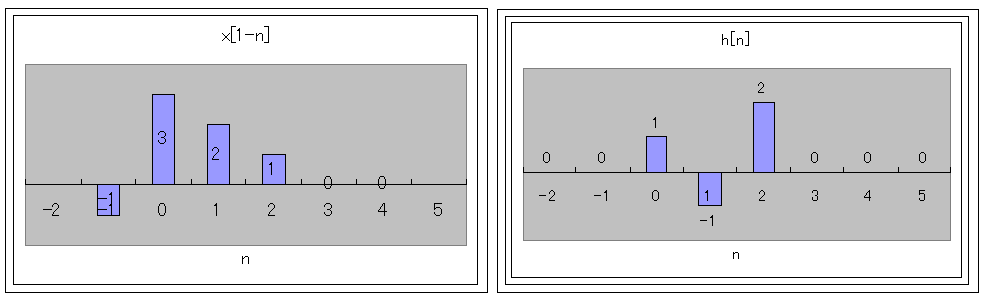
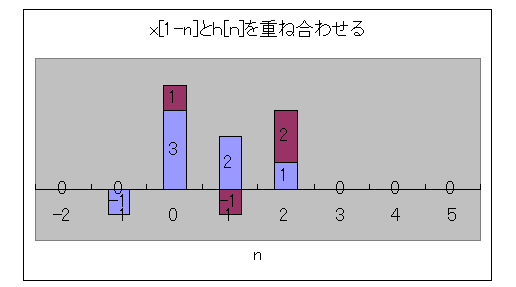
h[1-n]とx[n]を重ねてみましょう。

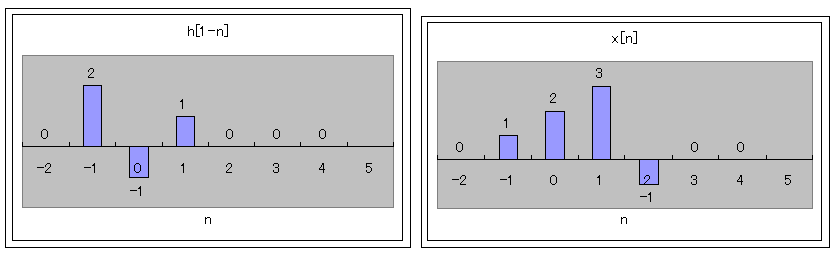


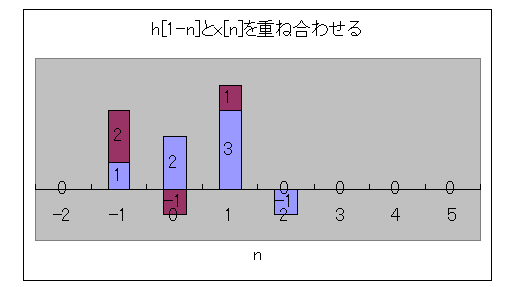
h[1-n]がアズキ色、x[n]が青、
そうしますと、
y[1]は、同じ位置の、アズキ色と、同じ位置のx[n]の掛け算で、求める事ができます。

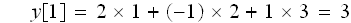
これは

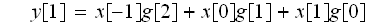
の図式的説明になります。
では

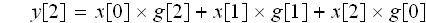
の図式的説明は? と言いますと
これは

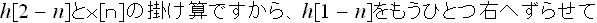


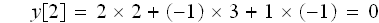

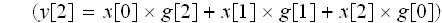


となります。

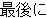

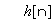 は、そのままで、x[n]を逆にする事を考えましょう。
は、そのままで、x[n]を逆にする事を考えましょう。







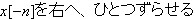



同じように、重なっている所を、掛け合わせます。

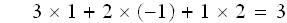
同じく、y[1]が求まりました。
y[2]も、x[1-n]を1つ、ずらせて、h[n]と重ねると



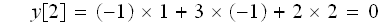


と、求まりました。
以上より

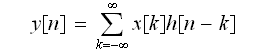
の式は

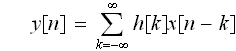
と、どちらででも、表されることになります。

普通は、下の式が使われる事が、多いそうです。
ちょっと、疲れたニャン。
[Introductory DIGITAL SIGNAL PROCESSING second edition Paul A.Lynn Wolfgang Fuerst p.32-50]
H.15.5.21
This document created by Scientific Notebook 4.1. この文書は次の製品で作成しました Scientific Notebook 4.1.