Z変換超入門 その１

今までは、時間軸についての考察でした。

Z変換なるものを使うと、周波数軸についての考察が、可能になります。

と、言うても、判りにくい（私にとって...）ので、

まずは、具体的に見ていきましょう。

１．Z変換の定義

ディジタル信号をx[n]として

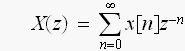
このX[ｚ]を、x[n]のZ変換と言います。

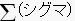でまとめちゃうと、簡潔できれいなんですが

具体的に考えると

ディジタル信号の各x[n]に、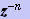をくっ付けただけのものです。

ですので

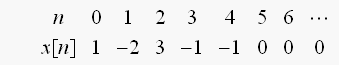
の信号があると、ｚ変換は

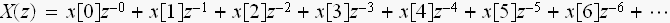
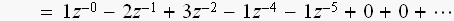
となります。

反対に 、ｚ変換の無限級数が

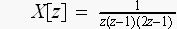
と表されていたとすると、

このを級数展開すると （これは、計算エンジンにやってもらいました。）

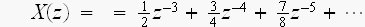
と、なるので

ここから、元の信号x[n]は

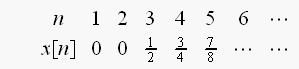
と、わかります。

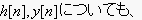同様に

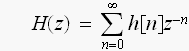
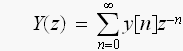
で、Z変換が定義されています。

２．Z変換すると、どんな良い事が？

１．シグナルと、その解析を周波数軸（フリケンシードメイン）で、考えることができる。

２．１つの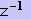は、サンプリング周期の１タイムシフトに相当する。

１．については、後ほど、例で考えてみましょう。

２．については

（引用 *三谷 「信号解析のための数学」p.51 森北出版 ）

まず、アナログ信号f(t)を、サンプリング周期がT秒のディジタル信号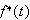に変換すると

(t<0に於いて f(t)=0と仮定すると）

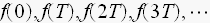
となり、

更に、デルタ関数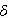で表現すると、ディジタル信号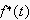は

(以前、x[n]の一般式を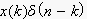と、置いたことと、似てますね。)

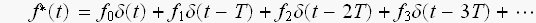
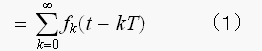ただし

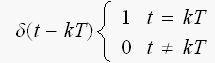
と、表現されます。

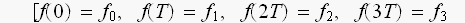な、訳です。]

ラプラス変換では 、

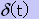「 のラプラス変換は １」

「T秒の遅れは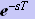を掛けることに等しい」

と、言うのが、ありました、よくわからんけれども...

ですので、上記のディジタル信号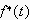を、ラプラス変換すると

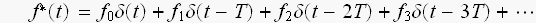
は

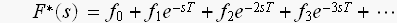
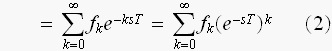
と、言う具合に、変換されちゃう訳です、きれいやなあ...

ここで

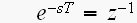
と言う置き換えをすると、

上の（２）式は

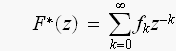
と書くことができます。

これは、ディジタル信号のZ変換の式、そのものです。

１サンプリング時間の遅れに相当する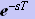を、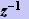に置き換えた！

そやから

Z変換は、ラプラス変換そのものやっ！

（「ラプラス変換そのもの」が、よう、解っとりませんが...(^_^;; ）

それで、

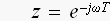
を代入すると、周波数特性が解る訳ですねっ。

（アナログの時に、ラプラスのｓに、ｓ＝ｊ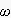を代入すると、周波数特性が出たように...）

三谷先生、ありがとうございます。

（アナログを調べていた時、Haywardさんの「Intorduction To Radio Frequency Design」に、出逢った時のように、

親切やっ！ ほんまに、......ありがとうございます。）

３．周波数軸で考えてみましょう

前節で、移動平均が、ローパスフィルターの働きをする事が、わかりました。

その事を調べてみましょう。

例

移動平均数が、５つの時、

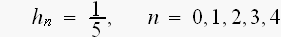
この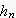を、Z変換すると

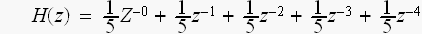
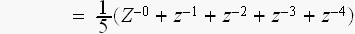
（ｈの係数に、ｚ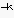掛けるだけで、できあがります。）

この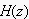が、実は、伝達関数になってます。（これは、後ほど...）

周波数特性を見るためには、先ほどの

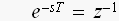
の、変換を行います。

ここで、サンプリング周期Tを１秒と仮定し（T=1)、ｓ＝ｊ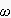を代入すると

H(z)の式は、変数が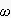となって

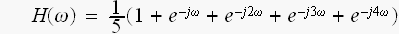
振幅の周波数特性を求めるには

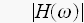
を、計算すれば、よいのです。

グラフを、計算エンジンに書いてもらいますと

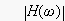
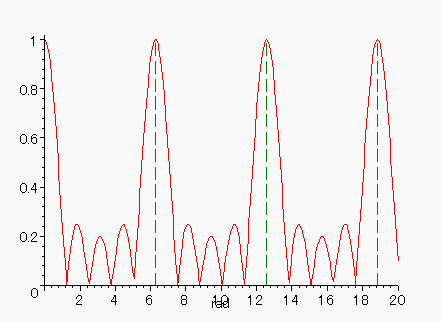
ｘ軸の単位は、ラジアン（rad）

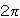ラジアン毎に、特性が繰り返されます。

ｘ軸が０から２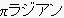の範囲に限局し、log表示しますと

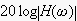
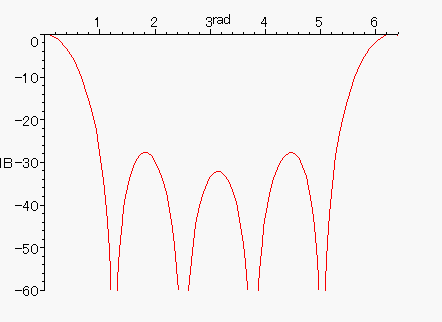
極を持った、ローパスフィルタである事が、わかります。

極の数は移動平均数に一致しています。

ここで、移動平均数を２０にすると、

伝達関数 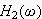は

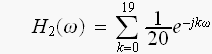
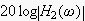
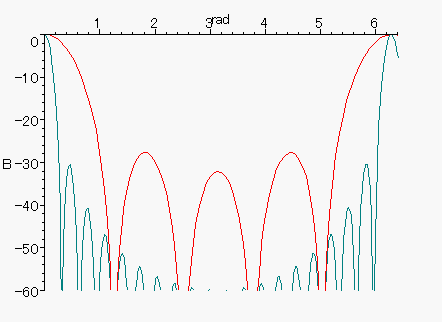
赤は移動平均数が５のH(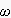)、緑が移動平均数２０の

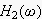
このようなグラフになり、

移動平均数を増やすと、振幅特性が、より鋭いローパスフィルタになる事が、わかります。

極の数は、やはり、移動平均数と一致しています。

H.15.6.11