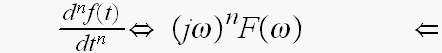フーリエ変換での時間微分、積分

（松尾せんせ「やさしいフーリエ変換森北出版」）

この性質は、デルタ変調、差分変調、FM変調、高域通過フィルタ、低域通過フィルタと、密接に関連があります。

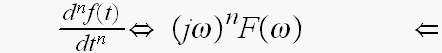むちゃ重要！

証明

$\vspace{1pt}$ 定義より

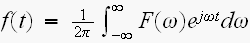
両辺をｔで微分すると

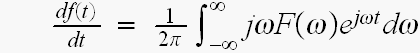
左辺と、右辺の積分の中の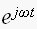 $e^{j\omega t}$ を除いたものがフーリエ変換対ですから

n=1の場合が求まったことになります。同様にして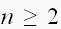 $n\geq 2$ の場合も求まります。」

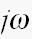これやがな、これが $j\omega$ を掛ける理由やったんや....なーる。

「（西城）ヒデキ、感激!」 (^_^;;

前々節の、「4.f(t)の導関数のフーリエ変換となっ？」は

同じ事を、言うてるねんな。

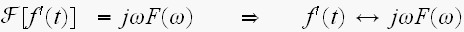
ちょっと、表現が違うと、もう、解れへんようになるねん....(T_T)

そいで、次に積分

（これは、前節のHeaviside関数のフーリエ変換が解ってないと、あかん）

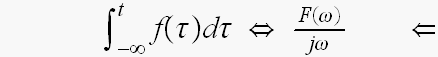やはり、めちゃ重要

証明（松尾せんせによる同著から）

「

$\vspace{1pt}$

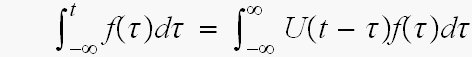
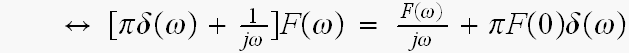
直流成分を除くとF(0)=0となって

」

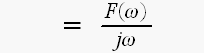U(t)：ステップ関数（＝Heaviside関数）

「なーるほど」とは、まだ、よう言わん。

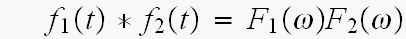の式

たたみ込みが、まだ、よう解ってへんから。

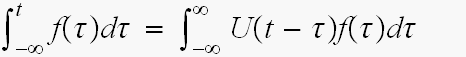２．なんで？

積分の範囲がｔから、 $\infty$ に変わってるよね。

何で、これが、できるかと、言うと、

ステップ関数(=Heaviside関数）を使うと、できるねんやわ。

のグラフが、下でしょ。
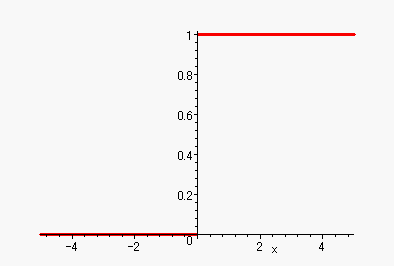
graphics/dsp69__18.gif

ほな、

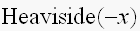
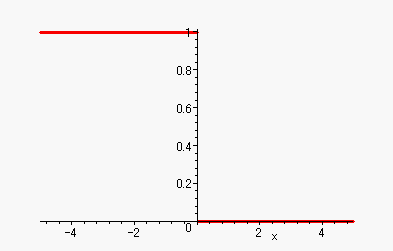
graphics/dsp69__20.gif

ほんで、これをずらすには、

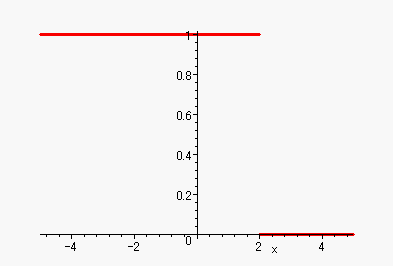
graphics/dsp69__22.gif

これと、関数ｆ（ｘ）を掛けた関数は、

２以上では、ゼロになるから

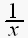
例えばｆ（ｘ）＝ $\frac{1}{x}$

と、すると

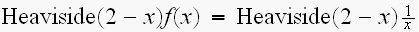
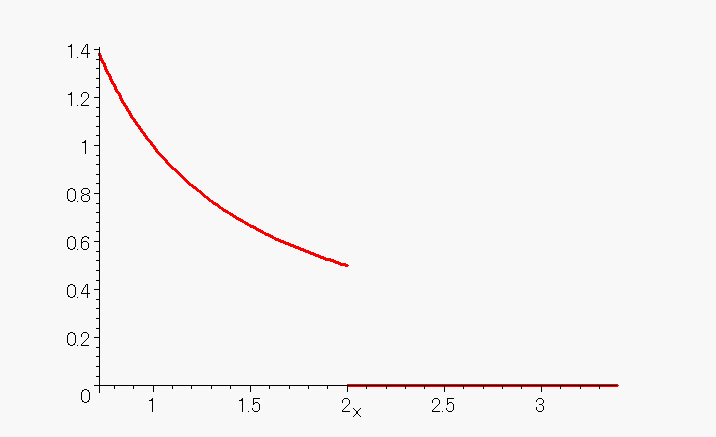
graphics/dsp69__25.gif

ｘが2以上では、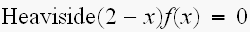と、なるから

積分の範囲を拡大して

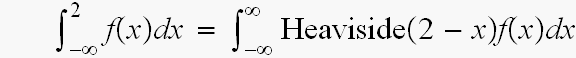
と、しても、ええ、ちゅう事になるやんか。

そしたら、たたみ込みの式になるので

たたみ込みの公式が、使えることになって便利やん...