サンプリングしてみる

１．単位インパルスの振幅は、なんぼなん？

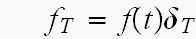
ｆ（ｔ）を、周期Tの間隔でサンプリングすると

サンプリングされた波形は

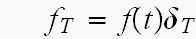
ｆ（ｔ）と、インパルス列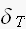 $\delta _{T}$ 、の積で表される。

ここに

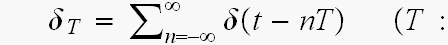サンプリング周期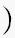

..........

ちょっと、解らんのは

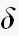デルタ関数 $\delta$ とは、単位インパルスの事

やったら、

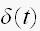$\delta (t)$ 関数の定義から言うたら、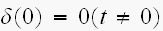やんか。

大きさが、わからん...

そやけど、今の場合、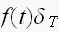 $f(t)\delta _{T}$ で、サンプリングされた波形を現してるから

どう考えても、

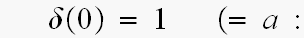実数でもええけど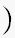

やと、思うけど....

それやったら、離散の式の時の、クロネッカーの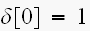

の事と、混同してるような気がする...（私は、当然、混同しとったわ...(^_^;; )

そこら辺が、解らんとこ、なんですけど...

んでも、今の場合、大きさ（振幅）は、問題ではなくて

周波数軸での間隔が、大きな意味を持つから。

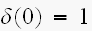
$\delta (0)=1$

で、考えていきます。

２．周波数軸では、どうなる？

サンプリングされた波形は

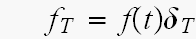
ですから、

たたみ込みの式より

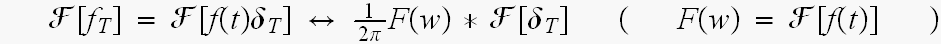
ここで、単位インパルスの列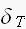 $\delta _{T}$ のフーリエ変換は

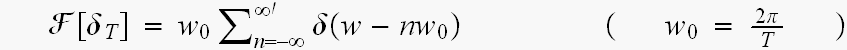
でした。

一方、一般的な、たたみ込みの式は

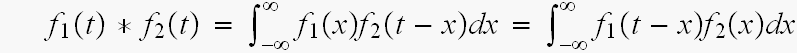
でした。

ところで、こんな、たたみ込みの式、ありましたっけ？

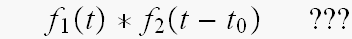
なんでか言うたら

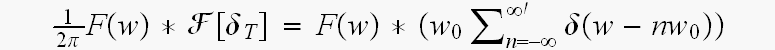
の、中で、第ｋ項のたたきこみで

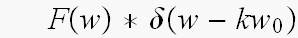
なんて、項が、出てくるんです。

4日ほど？？？状態(T_T)涙。

よーく、考えてみたら

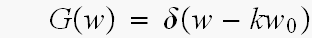
つまり、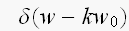は、G(w)の関数の中身なんでした...なはは..

だから、たたき込みは

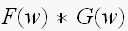$F(w)\ast G(w)$ の形なんでした。

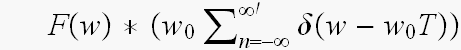
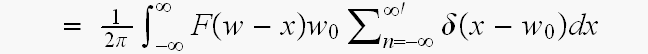
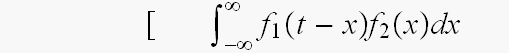の形

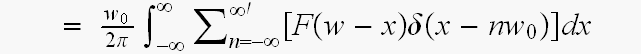
ここで、積分の中身は、

デルタ関数の定義

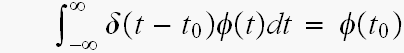
より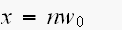 $x=nw_{0}\qquad$ の時だけ、値を持つから

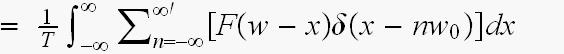
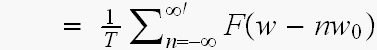
ふー、やれやれ、なんとか教科書通りに、なりました...

この結果を使って、周波数関係を、色々調べてみます。

続く....

大黒、ゴール！バンザーイ！ \(^_^)/