
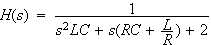
前回、Butterworth特性2次ローパスフィルタの正規化((normalize)で迷いました。
(実は、殆ど、normalizeできていた...)
2poleローパスフィルタの伝達関数は

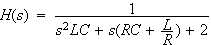
でした。
そして

 とおくと
とおくと
その振幅応答
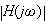 は
は

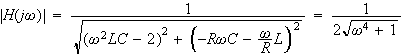
となり、ここで
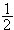 という係数が出てきたので
という係数が出てきたので
normalizeできていないと、迷ったのです。
実は、この係数
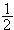 は、フィルタ特性
は、フィルタ特性

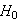 と呼ばれており(多分そうだと思う...)
と呼ばれており(多分そうだと思う...)

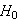 は、フィルタ利得と呼ばれてます。訂正します、なはは...。
は、フィルタ利得と呼ばれてます。訂正します、なはは...。
これで、normalizeできているようです。
入力と出力にresistance(抵抗成分)があれば、
フィルタを通した後の最大出力
は、
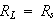 の時です。
の時です。
理由は
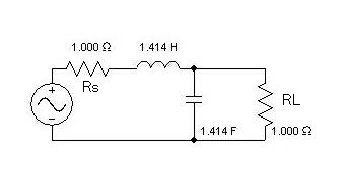
上図の、normalizeされた2次Butterworth特性ローパスフィルタ回路において
CとLはリアクタンス成分を持っており、このリアクタンス成分は
電流を妨げるから
この回路の最大出力は、リアクタンス成分がない時を考えればよい。
で、今、CとLがないと考えると,
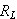 と
と
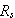 の直列回路となる。
の直列回路となる。
この時、出力
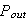 は
は

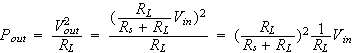

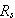 が一定のとき、
が一定のとき、
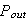 が最大になるのは、
が最大になるのは、
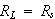 の時です。
の時です。
もし、
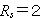 とすれば、
とすれば、
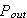 のグラフは
のグラフは

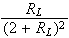
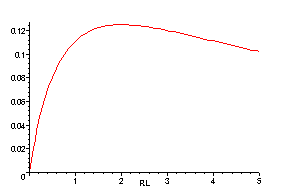
となり、
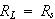 の時、
の時、
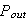 が最大になる。
が最大になる。
ですから、取り出せる最大出力は、入力の
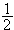 を越えない。
を越えない。
(電圧は、これより大きくなることも、十分ありますよね。)
この振幅応答
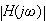 のグラフは、
のグラフは、
出力電圧が入力電圧の
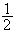 を0dBとして描かれているのだと思いますが
を0dBとして描かれているのだと思いますが
確信はありません...
正規化(normalize)とは、
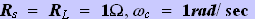 にすること
にすること
余計かもしれませんが、ローパスフィルタに限れば
回路内のCとLの数は、フィルタの次数と一致している
出力抵抗
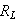 を
を
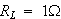 の時と
の時と
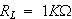 に変えた時の反射(reflection)を見てみました。
に変えた時の反射(reflection)を見てみました。
(振幅応答のグラフは、両者全く、同じなので...)
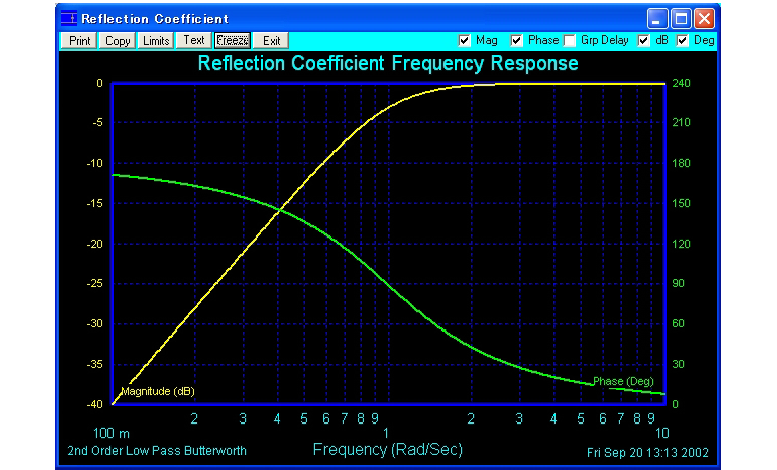

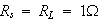 の時
の時
0dBは全反射です。
このグラフをみると、
1rad/secにおいて、-3dBですから、
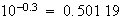 と、約半分の電力が戻ってきたことになります。
と、約半分の電力が戻ってきたことになります。
その分が出力として、取り出されたということになります。
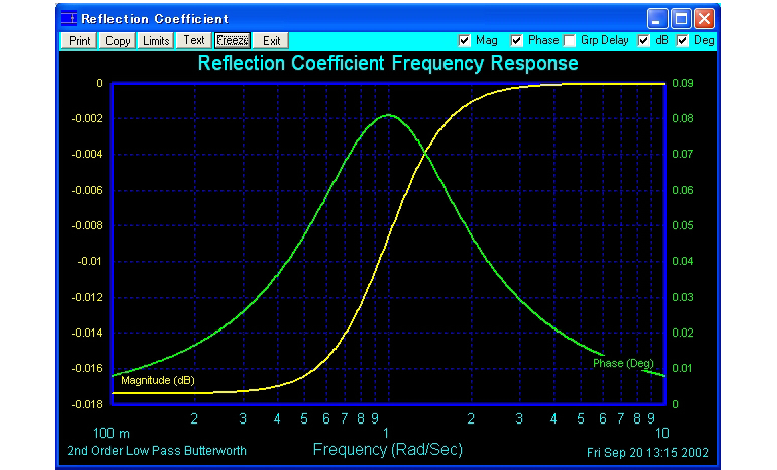
信号源が
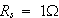 で、負荷が
で、負荷が
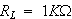 の時です。
の時です。
1rad/secにおいて、
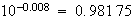 と、98%が戻って来たことになります。
と、98%が戻って来たことになります。
そして、通過帯域内に於いても、
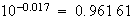 と、ほとんど、戻ってきています。
と、ほとんど、戻ってきています。
振幅応答のグラフの形は同じでも、ローパスフィルタになっていません。
もちろん、1 rad/secで-3dBのバターワースにも...
と言うことは
Xtalのラダーフィルタを作る時、
入出力端の抵抗を色々変えて、きれいな特性が出るようにしていますが
形はともあれ、
かなりのパワーロスを覚悟しなければなりません。
前節で
ノーマライズされた、n次のButterworth特性のフィルターの周波数特性は

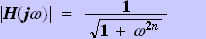 (2)
(2)
と表せ、この時のk番目のpoleの位置
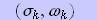 は
は

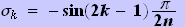

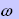 k
k


 という項目がありました。
という項目がありました。
これは、半径1の円を描き、この円を2n等分すると、バターワースの極が見つかると言うものです。
これで、n次の時のn個の極の位置がわかります。
そうすると、

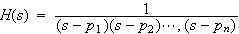
から、伝達関数
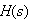 が求まります。
が求まります。
今、

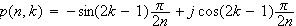
と置くと、
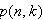 は、n次の時の極の位置を計算してくれます。
は、n次の時の極の位置を計算してくれます。



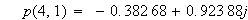

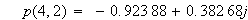

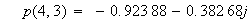

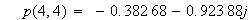


便利です。

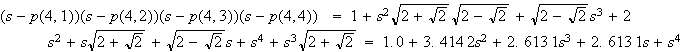
ですから

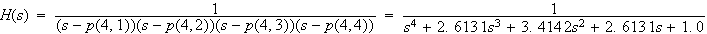
次は、規格化されたC,Lの値を求めることです。(Rは1と置く)
ありがたい公式があります。

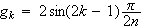
kはk番目のLかC
ここで

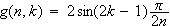
と定義すると

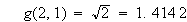

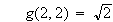



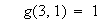

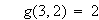

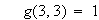



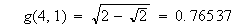

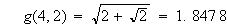

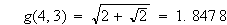

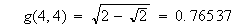


と言う具合です。
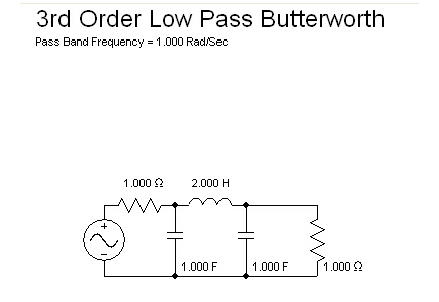
出典
Introduction to Radio Frequency DesignWes Hayward ARRL
トラ技Original No.9 CQ出版社
アナログ & ディジタルフィルタ入門 小野浩司 日刊工業出版社

