 嚁倎値丒倱倝値乮俶丒冎1丒倲+冇値乯
嚁倎値丒倱倝値乮俶丒冎1丒倲+冇値乯
旜敗OM偲偄偆曽傛傝丄僔儑僢僉儞僌側儊乕儖傪捀偒傑偟偨丅
丂
乽 偝偰丄婱揳偺HP傪攓尒偝偣偰捀偒丄彮偟栤戣揰傪傒偮偗傑偟偨丅
怣崋廃攇悢偺攞埲壓偺僒儞僾儕儞僌廃攇悢偱偼丄尦偺怣崋傪暅尦弌棃側偄偲偁傝傑偡偑丄
偙傟偼娫堘偄偱偡 丅乿
丂
丂
丂
壗搙偐丄巹偲偺丄儊乕儖偺傗傝偲傝偑丄偁傝傑偟偨偑
寢榑傪丄愭偵堷梡偝偣偰捀偒傑偡丅
丂
乽堦斒偵丄幚嵺偺僒儞僾儕儞僌丒僷儖僗偼師幃偱昞偝傟傞偼偢偱偡丅
僼乕儕僄揥奐偡傟偽
丂
S倫亖倎亄 嚁倎値丒倱倝値乮俶丒冎1丒倲+冇値乯
嚁倎値丒倱倝値乮俶丒冎1丒倲+冇値乯
丂
偺傛偆偵側傝傑偡丅
偙傟偲尨怣崋倐丒倱倝値乮冎2丒倲乯偲偺愊偑丄僒儞僾儕儞僌偝傟偨弌椡偱偡偐傜
丂
俷倀俿亖倐丒倱倝値乮冎2丒倲乯乮倎亄 嚁倎値丒倱倝値乮俶丒冎1丒倲+冇値乯乯
嚁倎値丒倱倝値乮俶丒冎1丒倲+冇値乯乯
丂
偲丄側傝
倎丒倐丒倱倝値乮冎2丒倲乯崁偼丄尨怣崋偦偺傕偺偺惉暘偵懠側傝傑偣傫丅
僒儞僾儕儞僌廃攇悢偵埶懚偟傑偣傫 丅
偨偩偟丄偪傚偆偳僒儞僾儕儞僌廃攇悢偑尨怣崋廃攇悢偺2攞偺偲偒丄
僒儞僾儕儞僌丒僷儖僗偺崅挷攇偲偺愊偑姳徛偡傞 偙偲偵側傝傑偡丅
偛懚抦偺傛偆偵丄愊偼榓偲嵎偺惉暘偵暘夝弌棃傞偐傜偱偡丅
偦傟偱偼丄堦斒偵尨怣崋偵0俫倸偐傜廃攇悢惉暘傪傕偭偰偄偨偲偟偨傜
傑偝偵丄尨怣崋偑娷傓嵟戝廃攇悢偺2攞埲壓偺僒儞僾儕儞僌廃攇悢偱偼丄偄偨傞偲偙傠偱姳徛傪偆偗偰偟傑偄傑偡丅
偙傟偑丄僒儞僾儕儞僌掕棟偺杮摉偺堄枴 偱偡 丅
屘偵丄尨怣崋傪拪弌弌棃側偄偲偄偆偙偲偵側傝傑偡丅
丂
偦傟偱偼丄尨怣崋偺廃攇悢惉暘偑0俫倸偐傜偱偼側偔丄傕偭偲崅偄廃攇悢偐傜懚嵼偟偰偄偨傜偳偆偱偟傚偆丅
応崌偵傛偭偰偼丄掅偄僒儞僾儕儞僌廃攇悢偱傕姳徛偟傑偣傫丅
弌棃傞応崌傕偁傝傑偡丅傑偨丄弌棃側偄応崌傕偁傝傑偡丅
弌棃傞偲偟偨傜丄僒儞僾儕儞僌廃攇悢偺斖埻偼丄偳偙偐傜偳偙傑偱側偺偐傪丄嬦枴偡傞昁梫偑偁傝傑偡丅
尨怣崋偺嵟戝廃攇悢偲丄懷堟暆偺斾偱寛傑傞丄偲巚偄傑偡丅
偦偺嬌尷偑丄僒僀儞攇偺僒儞僾儕儞僌偲偄偆栿偱偡丅...乿
丂
***丂嫮挷偟偨強偼丄巹偑丄彑庤偵峴偭偨傕偺偱偡丅丂***
丂
僒儞僾儕儞僌偡傞堊偺丄僀儞僷儖僗楍偺曽傪丄僼乕儕僄媺悢揥奐偡傞両
巹偼丄偁偭偝傝丄擺摼偱偒傑偟偨丅乮堦斢丄昁梫偱偟偨偑...乯
丂
埲忋偑丄寢榑偱偡丅
----------------------------------------------------------------------------------------------------------------------------------------
埲壓偼丄嵟弶偵捀偄偨儊乕儖偐傜敳悎偟傑偟偨丅 棟夝偺彆偗偵側傞偲丄巚偄傑偡偺偱...
丂
乽HP偱偼丄僒僀儞攇傪懳徾偵偟偰偄傑偡偺偱丄僗儁僋僩儖偵峀偑傝偼偁傝傑偣傫丅
偪傚偆偳丄攞偺廃攇悢偱僒儞僾儕儞僌偟偨帪偺傒姳徛偑婲偒傞偩偗偱偡丅
4.5KH倸偺尨怣崋傪丄8KH倸偱僒儞僾儕儞僌偟偨応崌偱傕傗偼傝丄4.5KH倸偺惉暘偼懚嵼偟傑偡丅
揔摉側僼傿儖僞傪擖傟傟偽丄拪弌偱偒傞偼偢偱偡丅偨偩偟怣崋偼丄彫偝偔側傞偺偑晛捠偱偡丅
丂
僒儞僾儕儞僌掕棟偺堄枴偡傞偲偙傠 偼
尨怣崋偺僗儁僋僩儖偵峀偑傝偑偁傞応崌乮惓妋偵偼0Hz偐傜惉暘傪娷傫偱偄傞応崌乯 傪丄偝偟偰偄傑偡丅
僔儞僌儖僩乕儞傗丄懷堟偑尷傜傟偰偄傞応崌偵偼丄傛偔嬦枴偡傞昁梫偑偁傝傑偡丅
摉曽偺SSB敪惗婍偼丄傑偝偵偙偺偙偲傪媡偵棙梡偟偰偄傑偡丅
丂
僒儞僾儕儞僌掕棟偼丄幚偵傛偔岆夝偝傟偰偄傑偡丅
戝妛偺愭惗曽偺挊彂偵傕丄忋婰偺偙偲偑丄柧妋偵愢柧偝傟偰偄側偄偺偑懡偄傕偺偱偡丅
偙傟偵偼丄杮摉偵傑偄傝傑偡丅
丂
壗偐偺堦偮妎偊偺傛偆偵丄偲偵偐偔丄尨怣崋偺攞埲忋偺僒儞僾儕儞僌廃攇悢偱側偗傟偽側傜側偄偲
怣偠偙傫偱偄傞曽偑懡偔 丄榖偟偑捠偠傑偣傫丅
...慜揷偝傫乮*巹偺帠乯偺傛偆偵丄曌嫮偟巒傔偺曽偵偼丄惀旕偲傕岆夝偝傟偨偔側偔丄梋寁側帠傪偄偄傑偟偨丅乿
丂
丂
乽*Steven巵偺彂愋偝偭偲撉傫偱傒傑偟偨丅僒儞僾儕儞僌掕棟偵偮偄偰偼
傗偼傝丄僒僀儞攇傪椺偵偲偭偰愢柧偝傟偰偄傞傛偆偱偡偹丅
僒儞僾儕儞僌廃攇悢偑掅偄偲丄掅偄廃攇悢偵曄姺偝傟偰偟傑偆偲偄偆傛偆側帠偩偲巚偄傑偡丅
巹偵尵傢偣傟偽丄偦傟偑偳偆偐偟偨偐偲尵偄偨偔側傝傑偡丅
僒儞僾儕儞僌廃攇悢偑崅偗傟偽丄崅偄廃攇悢惉暘偺傒偑丄尦怣崋惉暘偵忯廳偟偰偄傞偵夁偓偢
杮幙揑憡堘偼偁傝傑偣傫丅
僒儞僾儕儞僌廃攇悢偑掅偄応崌偱傕丄傗偼傝尦怣崋惉暘偼懚嵼偟傑偡丅
偦傕偦傕丄僒儞僾儕儞僌廃攇悢偑丄2攞悺慜傑偱尦怣崋偑懚嵼偟偰偄偰
2攞埲壓偵側偭偨偲偨傫偵徚偊偆偣偨傜偙傟偼儅僕僢僋偱偡丅
偡偽傜偟偄僼傿儖僞偺弌棃忋偑傝偱偡丅
恾夝偑偱偒傟偽丄娙扨側帠側偺偱偡偑丅
偦偆丄幚偵娙扨側偙偲側偺偱偡丅
丂
夝愢彂偱丄僔儞僌儖僩乕儞偽偐傝傪椺偵偲偭偨愢柧偵偼丄偆傫偞傝偱偡丅
偙傟傪怣偠偙傫偱偟傑偭偨妛惗偝傫払偼丄堦庬偺嫸怣幰偲側傝丄傕偆庤偺偮偗傛偆偑偁傝傑偣傫丅乿
丂
*The Scientist and Engineer's Guide to Digital Signal Processing by Steven W. Smith, Ph.D chapter 3.
丂
乽...奜崙彂偺傎偆偑夝傝堈偄柺傕妋偐偵偁傞傛偆偵巚傢傟傑偡丅偟偐偟丄扨弮側栤戣偱偼側偄傛偆偵巚傢傟傑偡.
壗傛傝傕栤戣偼丄悢幃傪尒敳偔栚傪梴偆偙偲偱偼側偄偐偲巚偄傑偡丅...乿
-------------------------------------------------------------------------------------------------------------------------------------------------------
------------------------------------------------------------------------------------------------------------------------------------------------------
埲壓偼丄巹偺丄傎傫傑偵愘偄丄乽僒儞僾儕儞僌掕棟傪棟夝偡傞偨傔偵乿峫偊偨帠偱偡丅
僒儞僾儕儞僌揰
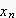 偼
偼



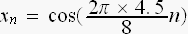
偐傜丄媮傔傞丅

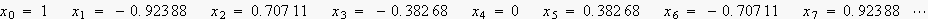


..


師偵丄偙偺僔儞僌儖僩乕儞傪亅
 偐傜亄
偐傜亄
 傑偱丄廃婜揑偱偁傞偲丄壖掕偟偰
basis functions偲偺correlation偱偁傞 ,DFT傪峴偆丅
傑偱丄廃婜揑偱偁傞偲丄壖掕偟偰
basis functions偲偺correlation偱偁傞 ,DFT傪峴偆丅

 [INTRODUCTORY
DIGITAL SIGNAL PROCESSING Paul A.Lynn Wolfgang Fuerst p.67偺岞幃偐傜乮3.1乯丄乮3.2乯傪敳悎]
[INTRODUCTORY
DIGITAL SIGNAL PROCESSING Paul A.Lynn Wolfgang Fuerst p.67偺岞幃偐傜乮3.1乯丄乮3.2乯傪敳悎]
丂

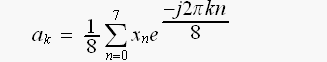 (3.1)
(3.1)丂

![]()

![]()


偦偟偰丄偙偙偐傜丄嵞傃
尦偺僒儞僾儕儞僌攇宍(
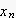 )偺暅尦丄
)偺暅尦丄

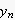 傪丄媮傔偰傒傑偡丅
傪丄媮傔偰傒傑偡丅



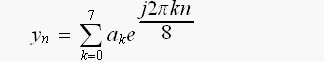 (3.2)
(3.2)
 傕偟丄
傕偟丄
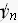 偑丄
偑丄






|
僌儗乕偑尦偺楢懕側4.5Hz丄椢偑丄  丄偦偟偰愒偺攋慄偑丄暅尦偟偨 丄偦偟偰愒偺攋慄偑丄暅尦偟偨  |
2廃婜栚偼丄堘偄偑偁傞偑丄1廃婜栚偼丄
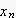 偲
偲
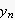 偼丄姰慡偵堦抳偟偰偄傞丅両
偼丄姰慡偵堦抳偟偰偄傞丅両
俉Hz偱僒儞僾儕儞僌偝傟偨丄4.5Hz偼丄1廃婜栚偼丄姰慡偵暅尦偝傟偰偄傑偡丅
2廃婜栚偼丄悢抣偼摨偠偱偡偑丄晞崋偑媡偱偡丅
偙偺丄1廃婜栚丄2廃婜栚傪侾偮偺扨埵偲偟偰丄埲崀丄偙偺扨埵偱孞傝曉偟傑偡丅
偱偡偺偱丄2廃婜栚偺晞崋傪媡偵偟偰傗傟偽丄
暅尦偟偨僒儞僾儕儞僌揰(
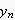 )偼丄尦偺僒儞僾儕儞僌揰(
)偼丄尦偺僒儞僾儕儞僌揰(
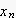 )偲丄姰慡偵丄堦抳偟傑偡丅
)偲丄姰慡偵丄堦抳偟傑偡丅
乽4.5KH倸偺尨怣崋傪8KH倸偱僒儞僾儕儞僌偟偨応崌偱傕
傗偼傝4.5KH倸偺惉暘偼懚嵼偟傑偡丅乿乮旜敗OM乯
偙傟偼丄
![]() 傪媮傔傞偲尵偆丄堄枴偱偼側偄偲丄巚偄傑偡丅
傪媮傔傞偲尵偆丄堄枴偱偼側偄偲丄巚偄傑偡丅
乮8Hz偺basis functions 偵丄4.5Hz偼丄側偄偐傜乯
4.5Hz偺僔儞僌儖僩乕儞傪丄8Hz偱僒儞僾儕儞僌偡傞偲丄
DFT偺寢壥偼丄4.5Hz傪basis funtions偱揥奐偟偨學悢
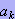 偑懚嵼偡傞偽偐傝偱偼側偔丄
偑懚嵼偡傞偽偐傝偱偼側偔丄
媡DFT偟偰傕丄1廃婜栚偼丄惓偟偔丄尦偺僒儞僾儖揰偲堦抳偟偰偄傞両両両


偙偺丄1廃婜栚偲丄2廃婜栚偱晞崋偑曄傢偭偰丄尦怣崋偑丄惓妋偵嵞尰偱偒側偄帠偵娭偟傑偟偰偼丄
旜敗OM偵夝寛偟偰捀偒傑偟偨丅



 乽4.5Hz傪8Hz偱僒儞僾儕儞僌偟偨応崌丄
乽4.5Hz傪8Hz偱僒儞僾儕儞僌偟偨応崌丄

 僒儞僾儕儞僌悢8偱偼丄4.僾儔僗0.5廃婜暘偲側偭偰偟傑偄傑偡丅
僒儞僾儕儞僌悢8偱偼丄4.僾儔僗0.5廃婜暘偲側偭偰偟傑偄傑偡丅

 僒儞僾儕儞僌偝傟傞懁乮偙偺応崌偼4.5Hz乯偼丄惍悢廃婜暘偱側偗傟偽側傝傑偣傫丅
僒儞僾儕儞僌偝傟傞懁乮偙偺応崌偼4.5Hz乯偼丄惍悢廃婜暘偱側偗傟偽側傝傑偣傫丅

 傛偭偰丄僒儞僾儖悢傪16傑偱憹傗偣偽9廃婜暘偲側傝OK偱偡丅
傛偭偰丄僒儞僾儖悢傪16傑偱憹傗偣偽9廃婜暘偲側傝OK偱偡丅

 4.5廃婜暘偱偁偭偨偨傔偵丄僾儔僗儅僀僫僗偑曄傢偭偰偟傑偭偨偺偱偡丅乿乮旜敗OM乯
4.5廃婜暘偱偁偭偨偨傔偵丄僾儔僗儅僀僫僗偑曄傢偭偰偟傑偭偨偺偱偡丅乿乮旜敗OM乯



 偆乕傫丄偦偆傗偭偨傫偐....惉傞掱偱偡丅壗搙傕丄偁傝偑偲偆偛偞偄傑偡丅m(_
_)m
偆乕傫丄偦偆傗偭偨傫偐....惉傞掱偱偡丅壗搙傕丄偁傝偑偲偆偛偞偄傑偡丅m(_
_)m
妋擣偟偰偍偒傑偟傚偆丅
乽4.5Hz傪8Hz偱僒儞僾儕儞僌偡傞乿  仺
乽9Hz傪16Hz偱僒儞僾儕儞僌偡傞乿
仺
乽9Hz傪16Hz偱僒儞僾儕儞僌偡傞乿
 丂
丂 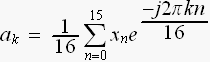
 丂
丂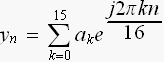

 尦偺僒儞僾儕儞僌揰
尦偺僒儞僾儕儞僌揰
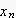

![]()



![]()

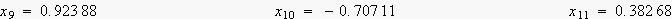

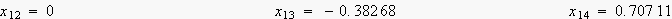

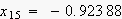


 暅尦偟偨僒儞僾儕儞僌揰y
暅尦偟偨僒儞僾儕儞僌揰y


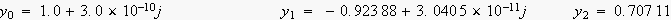

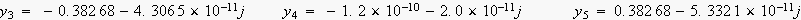

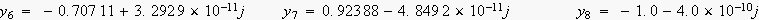

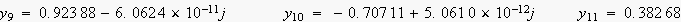

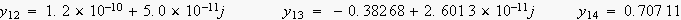

 乮寁嶼寢壥偼丄娵傔偢偵丄偦偺傑傑宖嵹偟傑偟偨丅乯
乮寁嶼寢壥偼丄娵傔偢偵丄偦偺傑傑宖嵹偟傑偟偨丅乯


尒帠偵堦抳偟傑偟偨丅
嵞搙屼楃怽偟忋偘傑偡丅
丂
僒儞僾儕儞僌揰
 偼
偼


偐傜丄媮傔傞丅
丂

 廃攇悢
0,1,2,3,4,5,6,7Hz偺奺惉暘
廃攇悢
0,1,2,3,4,5,6,7Hz偺奺惉暘
丂

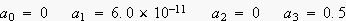

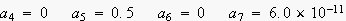
丂
暅尦偟偨僒儞僾儕儞僌揰









尦偺僒儞僾儕儞僌揰

![]()



![]()

![]()



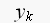 偲丄傕偲偺僒儞僾儕儞僌揰
偲丄傕偲偺僒儞僾儕儞僌揰
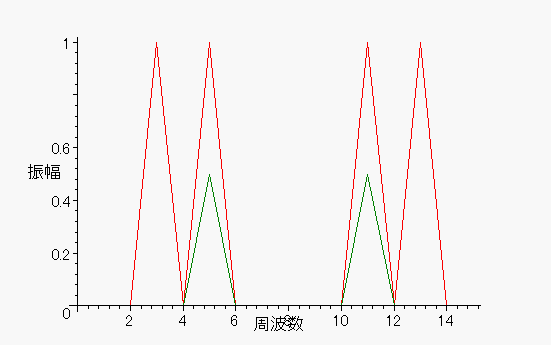
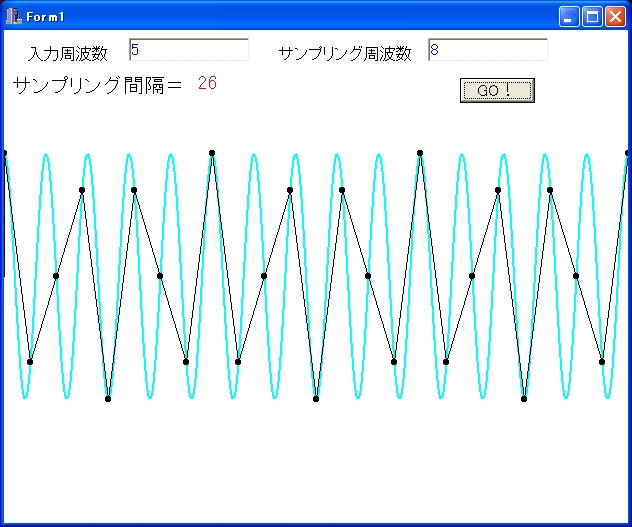
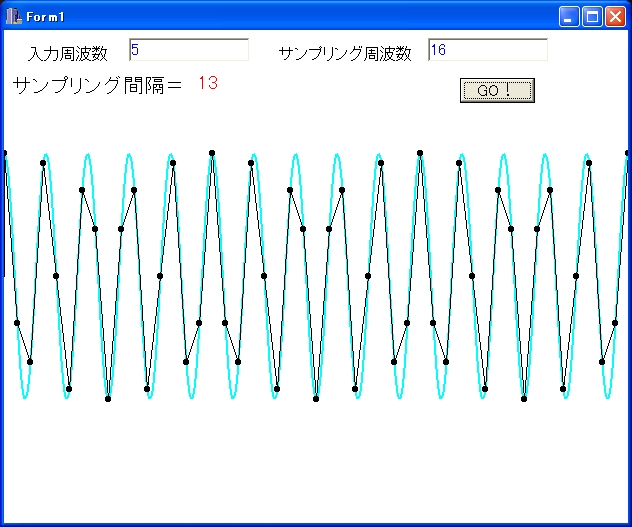
愒偼5Hz傪俉Hz偱僒儞僾儕儞僌丄椢偼5Hz傪16Hz偱僒儞僾儕儞僌偟
怳暆偺暘晍傪尒偨傕偺偱偡丅
乮僗儁僋僩儖偵丄峀偑傝偼丄偁傝傑偣傫偑丄尒傗偡偄偺偱丄偙偺傛偆偵丄慄偱寢傃傑偟偨丅乯
丂
偆傑偔丄昞尰偱偒側偄偺偱偡偑丄
乽傕偟丄
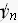 偑丄
偑丄
![]() 偲丄堦抳偡傟偽丄惓偟偔僒儞僾儕儞僌偝傟偨偲丄夝庍偝傟傞丅乿
偲丄堦抳偡傟偽丄惓偟偔僒儞僾儕儞僌偝傟偨偲丄夝庍偝傟傞丅乿
乮帪娫幉偐傜丄廃攇悢幉偵堏偟丄嵞傃帪娫幉偵栠偟偰丄暅尦偟偨僒儞僾儕儞僌揰偑
尦偺僒儞僾儕儞僌揰偲丄堦抳偡傟偽丄惓偟偔僒儞僾儕儞僌偝傟偨偙偲偵丄側傝傑偣傫偐丠乯
丂
偙偺娤揰偐傜尒傞偲丄乽5Hz偼8Hz偱惓偟偔僒儞僾儕儞僌偝傟偨乿偲偄偆帠偵側傝傑偡丅
僄僀儕傾僔儞僌偺3Hz偺懚嵼偑栤戣偲側傞乮尨怣崋偵側偄傕偺偑偁傞乯偲偡傟偽丄
偳偆偟偰丄5Hz傪16Hz偱僒儞僾儕儞僌偟偨帪偵丄11Hz偑懚嵼偡傞乮尨怣崋偵側偄乯偙偲偑
栤戣偵側傜側偄偺偱偟傚偆丠
丂
偳偪傜偺応崌傕丄棧嶶壔偵敽偆昁慠偩偲丄巚偆偺偱偡偑....
偲偵偐偔丄尨怣崋惉暘偼丄娷傑傟偰偄傞偙偲偑夝傝傑偟偨丅
丂
傑偩傑偩丄媈栤揰偑偄偭傁偄偱偡丅
丂
僨傿僕僞儖怣崋張棟傪丄挷傋巒傔偰丄3儢寧
恀悜偺堦抂偵怗傟傞帠偑偱偒丄姶寖偟偰偍傝傑偡丅
旜敗條偵偼丄怱偐傜丄屼楃怽偟忋偘傑偡丅


H15.07.07
丂



