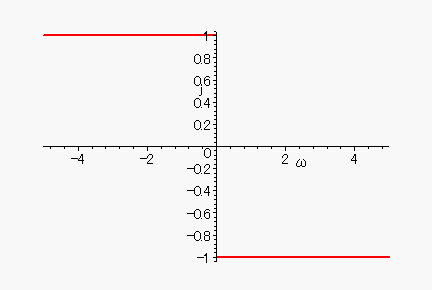
(・.2 離散的ヒルベルト変換器の周波数特性 C言語によるディジタル信号処理入門 三上直樹先生 CQ出版社 p.186より)
自分なりに調べてみました、心細いわ...
2.ヒルベルト変換の周波数領域での関係式
(ディジタル、アナログ信号処理のための やさしいフーリエ変換 松尾博先生 森北出版 p.56。
松尾先生が、式も書いて下さっています、私にゃ、とても無理です。)
「信号f(t)が因果性であるとき、そのフーリエ変換F(
![]()
互いに従属になることは第2章で述べましたが、ここでは
![]()
変換式を導きます。f(t)が因果性であることより、
これをフーリエ変換して




故に



![]()
故に


故に

故に

上式の実数部と虚数部に分けて


または、重畳積分を入れかえて


となります。 」
ふー、ここまで来るのに、随分時間が...
式を追うのが精一杯です。意味も、よう、解りもしませんわ...
松尾先生が、ヒルベルト変換について、お書きになっておられるのは、ここまでです。
(もっと、大切な、根本的な事を、いっぱいお書きになって居られます。)
しかたが、ないので、私、自分の超浅学も省みず、この事をやってみました。
きっと、とんでもない間違い、トンチンカンな事をしでかしていると思います。
ご指摘いただけましたら、誠にありがたいです。
合っているかどうか、自分でも、解らないのです...全く自信なし
松尾先生の、お導き下さった式

から、出発します。
フーリエ逆変換の定義より

ここに、
![]()



積分の順序を、入れ換えて





![]()



[wは、tの間違いです、すんません]



メープルに、解いてもらったのです。


そして、r(t)は、因果性でしたから、t>0の範囲だけ考えれば、上式は


という、恐ろしい数式になります、アジャパー!(伴・ 三郎さんのせりふ。左朴全さんの「ずびずばー」みたいなものです。)
上式は、r(t)が、どんな周波数であろうと、(-j)を掛ければよいのですから、
最初のヒルベルト変換の周波数特性と、一致します。
しかし、ほんまに、これでいいのでしょうか?
まったく、自信ありません....
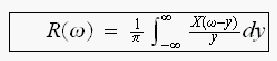
この式なのですが、
これは、周波数領域での重畳積分の式である事が、後ほど解ってきました。
そこで
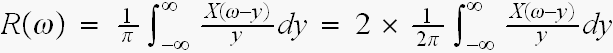
ですので
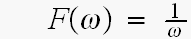
と、置きますと

のフーリエ変換対が、成り立つとして
上式は
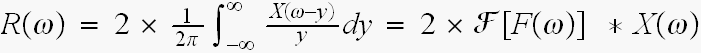
----
ここは1/2πが入ります、それとF(ω)の間違いです。
ですから
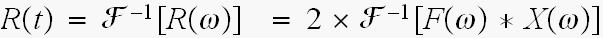
----
ここは1/2πが入ります。
ところで、一般に
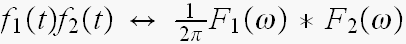
の関係が、ありますから
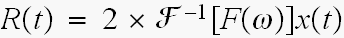
ここで
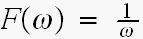
と、先に定義致しましたから
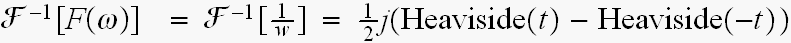
ですので
結局
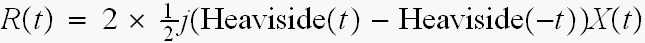
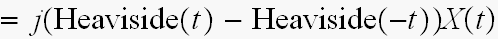
と、なります。
x>0の範囲を採れば
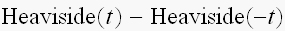
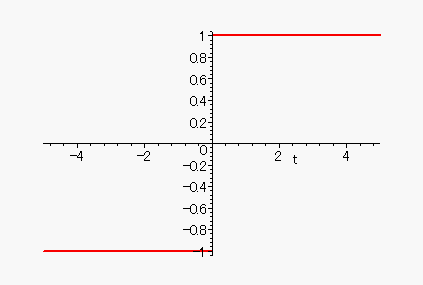
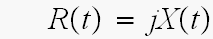
と、言う結論です。
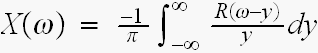
に、付きましては
同様にして
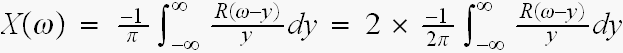
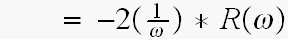
-------
ここは1/2π が入ります。
より
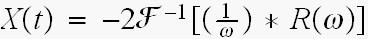
---
ここは1/2πが入ります。
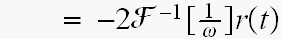
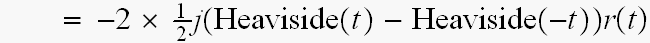
より,t>0の範囲では
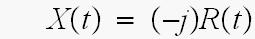
が、導かれます。
何とか、合っていたようで、ふー、やれやれです。(^_^);;
4.その他
べき級数で、関数を表現するよりも、三角級数で表現した方が、何かと都合が、よさそう..
.(お世話になったサイト http://www.ykt.info.gifu-u.ac.jp/dsp/sp3.pdf 解らないところが、殆どです...)
参考図書
「キーポイント フーリエ解析 船越満明先生 岩波書店」
「ディジタル.アナログ信号処理のための やさしいフーリエ変換 松尾博先生 森北出版」
「C言語によるディジタル信号処理入門 三上直樹先生 CQ出版」「フーリエの冒険 ヒッポファミリークラブ刊」
諸先生、ホームページをお書きくださっている皆様に、御礼申し上げます。 m(__)m
H.16.1.11
