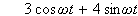1. 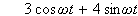は、どんな波形？

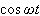を複素表示になおすと、すっごく計算しやすい。

複素表示の定義は

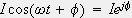
ですので

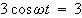
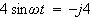
となるから

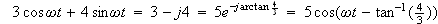
です。

これは、元の波形 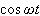に比べて

振幅は 5倍

位相は 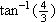ラジアンだけ、遅れている波形と読めます。

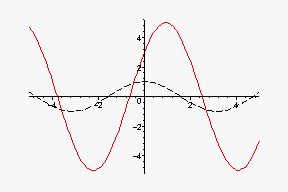
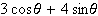の波形が赤実線、 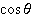の波形が黒点線でプロットしてみました。

参考書籍 「信号解析のための数学」 三谷政昭著 森北出版 p.14

2.コンデンサ、コイル等を含む回路の計算に、これらを複素表示したほうが

計算が楽ですし、見通しがよくなります。

微分をすることは、複素数の世界では、 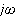を掛けることに等しい！

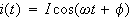とすると、

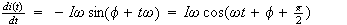(1)

ここで、i(t)を複素表示します。

複素表示の定義は

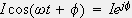
ですので

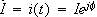
ですから、(1)式は

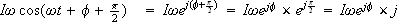
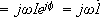
となり

微分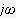＝ を掛ける

が成り立ちます！

ほんじゃ、積分は？

やってみましょう

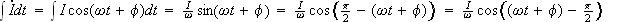(2)

ここで、cosは遇関数（cosA=cos（-A））を使いました。

(2)式は複素表示だと

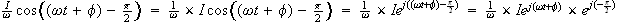
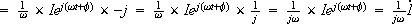
となり

積分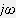＝で割る！

と言うことですね、ウーム...

3.コイルLと、コンデンサCの複素表示は？

コイルLの関係式は

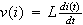
ですから、先ほどの、微分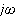＝ を掛けると使い、

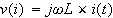
となりますので、オームの法則から類推して

コイルの抵抗（インピーダンス）は 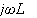です。

一方、コンデンサーCは

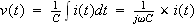
となり、同じくインピーダンスは 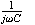となります。

次回は、これを使って、回路をしらべます。